매일 성장하는 블로그

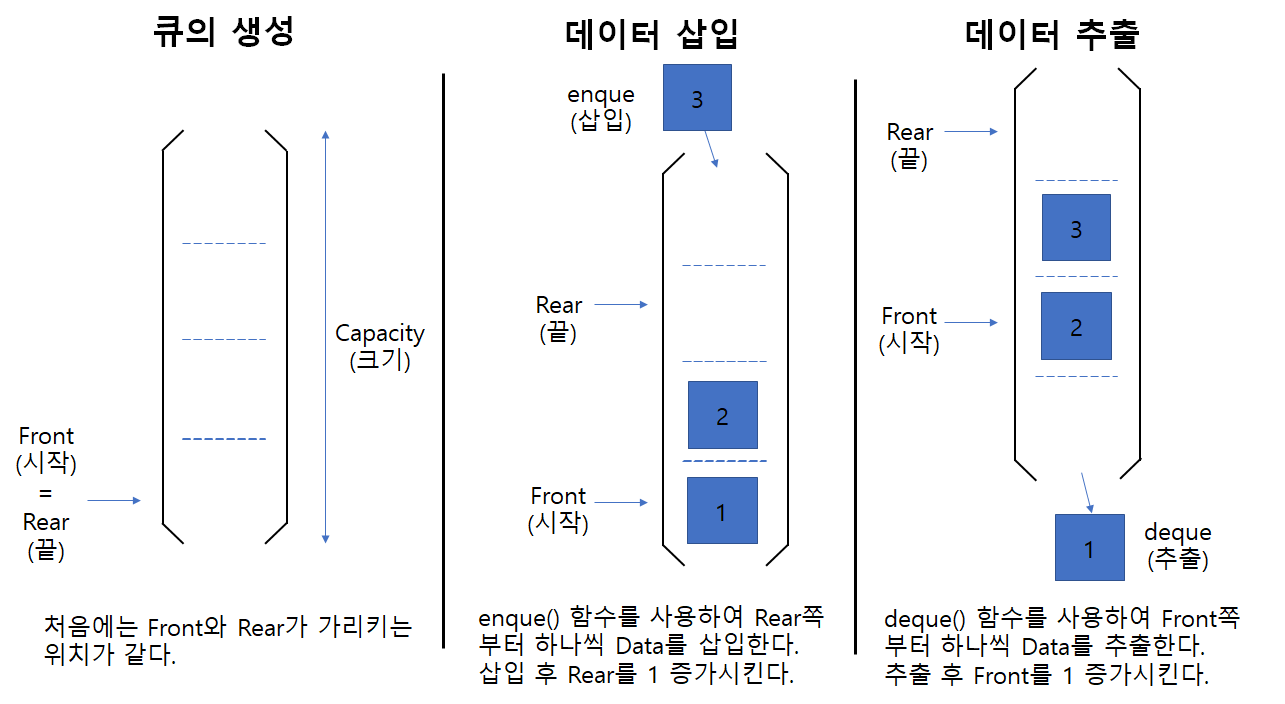
위상 정렬이란, 비순환 방향 그래프를 순서대로 정렬하는 방법이다.

1. 위상 정렬 조건

* 비순환 : 그래프에 시작과 끝이 존재해야 한다.(순환 가능하면 안된다.)

* 방향성 : 노드들 사이에 방향이 존재해야 한다.

2. 위상 정렬 특성

* 위상 정렬을 사용하여 정렬된 결과는 여러가지가 있을 수 있다.

3. 방법

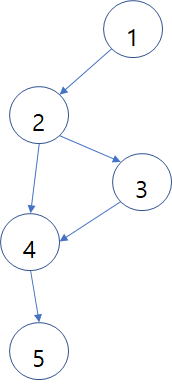
위와 같은 그래프의 모든 노드를 방향에 따라 순서대로 방문한다고 할 때, 위상 정렬은 아래와 같은 간단한 성질을 이용한다. 

특정 노드로 들어오는 간선(Edge)이 없다면, 방문 가능한 상태이다.

위의 성질을 이용하여, 아래와 같이 구현할 수 있다.

1. 방향 정보를 저장하는 배열을 생성한다.

주어진 방향 정보 : (1 → 2), (2 → 3), (2 → 4), (3 → 4), (4 → 5)

dir_list = [[1, 2],[2,3], [2,4], [3,4], [4,5]]

2. 각 노드들로 들어오는 간선의 개수(진입 차수)를 저장한다.

ex) 1번 노드로 들어오는 간선 : 0개

     2번 노드로 들어오는 간선 : 1개

     3번 노드로 들어오는 간선 : 1개

     4번 노드로 들어오는 간선 : 2개

     5번 노드로 들어오는 간선 : 1개

inDegree = [0, 1, 1, 2, 1]

3. 빈 큐를 생성하고, 들어오는 간선의 개수가 0인 노드들을 추가한다.

4. (Loop Start) 큐에서 순차적으로 deque한다.

5. deque된 노드에 연결된 간선들을 제거한다.(= inDegree 배열을 업데이트한다.)

6. 각 노드로 들어오는 간선의 개수(진입차수)가 0인 노드를 큐에 추가한다.(Loop End)

5. deque된 순서대로 출력한다.

위의 예시로 순차적으로 진행해보자.

[t = 0] : 초기 Set-up

1) inDegree 배열에서 들어오는 간선의 수(진입차수)가 0인 노드인 1번 노드를 찾아 큐에 추가한다.

[t = 1] : Loop Start

1) 큐에서 가장 왼쪽에 있는 노드를(1번 노드) deque한 뒤, 1번 노드에 연결된 간선들을 제거한다.

2) 들어오는 간선이 0이 된 2번 노드를 큐에 추가한다.

[t = 2]

1) 큐에서 가장 왼쪽에 있는 노드를(2번 노드) deque한 뒤, 2번 노드에 연결된 간선들을 제거한다.

2) 들어오는 간선이 0이 된 3번 노드를 큐에 추가한다.

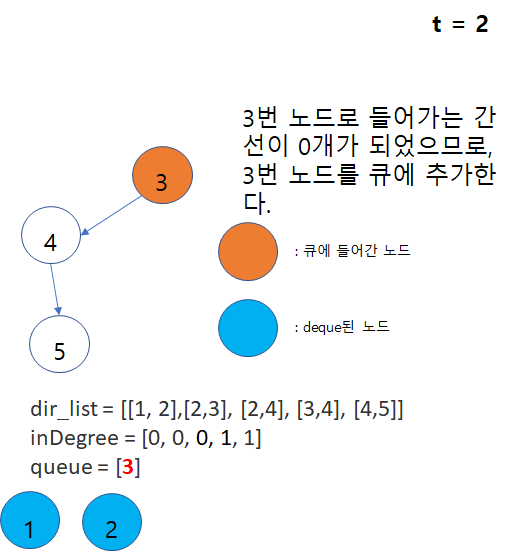
[t = 3]

1) 큐에서 가장 왼쪽에 있는 노드를(3번 노드) deque한 뒤, 3번 노드에 연결된 간선들을 제거한다.

2) 들어오는 간선이 0이 된 4번 노드를 큐에 추가한다.

[t = 4]

1) 큐에서 가장 왼쪽에 있는 노드를(4번 노드) deque한 뒤, 4번 노드에 연결된 간선들을 제거한다.

2) 들어오는 간선이 0이 된 5번 노드를 큐에 추가한다.

[t = 5]

1) 큐에서 가장 왼쪽에 있는 노드를(5번 노드) deque한 뒤, 5번 노드에 연결된 간선들을 제거하려고 보니, 제거할 것이 없다. 그대로 deque한다.

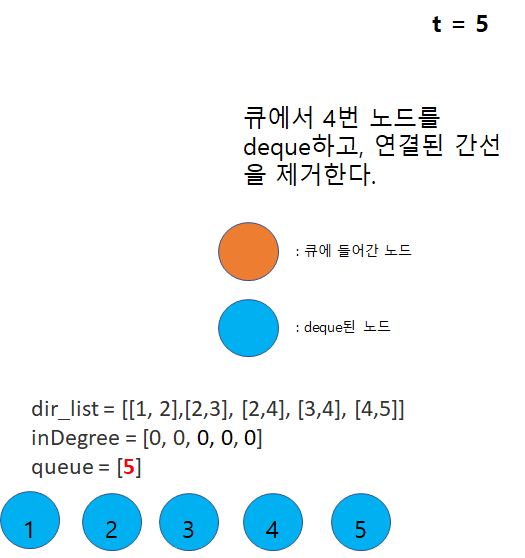
아래 deque된 노드들을 그대로 출력하면 위상정렬이 완료되었다. 결과는 [1, 2, 3, 4, 5]이다. 

이 그래프의 경우는 답이 한가지밖에 나오지 않지만, 아래와 같은 그래프는 위상정렬하면 여러가지의 결과가 나올 수 있다. 처음 시작을 6에서 해도 되고 1에서 해도 되기 때문이다.

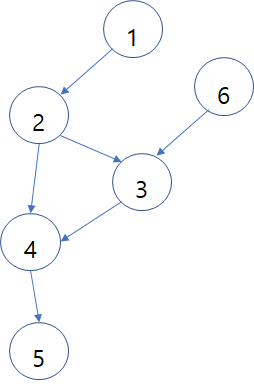
가능한 결과 : [1, 6, 2, 3, 4, 5], [6, 1, 2, 3, 4, 5]

위상정렬을 파이썬으로 구현하면 아래와 같다.

# n은 노드의 개수, m은 간선의 개수
# 생각의 편의를 위하여 0번 index는 비워놓고 진행

n,m = map(int, r().split())
inDegree = [0 for i in range(n+1)]
dir_list = [[] for i in range(n+1)]

for i in range(m):
    s, e = map(int, r().split())
    dir_list[s].append(e)
    inDegree[e] += 1

q = deque()

while True:
    for i in range(1, n+1):
        if inDegree[i] == 0:
            q.append(i)
    for i in range(1,n+1):
        x = q.popleft()
        answer.append(x)
        for j in dir_list[x]:
            inDegree[j] -= 1
            if inDegree[j] == 0:
                q.append(j)
    if not q:
        break
print(*answer)

BFS : Breadth-First Search(너비 우선 탐색)

DFS : Depth-First Search(깊이 우선 탐색)

최단 경로나 순위 선정 같은 문제에서 만날 수 있는 탐색 알고리즘들이다.

그래프의 개념과 표현법(인접 리스트, 인접 행렬)에 대해서는 아래 글을 참고하면 된다.

one-step-a-day.tistory.com/116

간단한 예시를 통해 각 방법이 어떻게 그래프를 탐색하는지 보자.

아래와 같이 트리가 주어진다고 하자.

BFS와 DFS를 사용하여 전체 트리를 탐색하는 과정을 보자. 특정 노드에 도착하면 노드의 색을 칠한다.

BFS(Breadth-First-Search) : 너비 우선 탐색

  주어진 트리를 BFS로 방문하는 과정은 위 그림과 같다. BFS의 경우 Level을 기준으로 탐색을 진행하게 된다.

Level 1 탐색이 완료되면 Level 2를 순차적으로 탐색하고, Level 2 탐색이 완료되면 Level 3를 탐색한다. (이 때 각 Level에서 오른쪽부터 검색할지, 왼쪽부터 검색할지는 알고리즘에 따라 달라진다.)

위와 같은 탐색을 진행하려면 다음과 같이 시작하면 된다.

1. 시작 노드를 방문한다.(Level 1)

2. 방문한 노드의 자식 노드들을 추가한다.(Level 2)

3. 추가된 자식 노드들을 차례로 방문하며 손자 노드들을 추가한다(Level 3)

4. 추가된 손자 노드들을 차례로 방문한다.

위와 같은 기능은 큐로 아래와 같이 구현할 수 있다.

1. 우선 빈 큐를 생성한 뒤 시작 노드를 추가한다.

2. 큐가 비어있지 않은 경우 아래 과정을 반복한다.

3. (Loop Start) 큐에서 Dequeue한다.(큐의 Front에 있는 원소를 pop) 

4. Dequeue한 원소의 자식 노드들을 큐에 append한다. (Loop end)

5. 큐가 비어있으면 종료한다.

위를 코드로 구현하면 아래와 같다. Visited를 표시하는 이유는 방문한 곳을 다시 방문하지 않기 위함이다.

(하나의 자식 노드가 2개의 부모 노드를 갖는 경우 중복 탐색이 발생할 수 있다.)

def bfs(arr, start):
    visited = defaultdict(bool)
    deq = deque([start])
    answer = []
    visited[start] = True
    while deq:
        x = deq.popleft()
        answer.append(x)
        for i in v_list[x]:
            if visited[i] == False:
                visited[i] = True
                deq.append(i)
    return answer

DFS(Depth-First-Search) : 너비 우선 탐색

BFS는 트리의 Level 순서대로 방문하는 알고리즘이었다면, DFS는 경로 순서대로 끝까지 탐색하는 알고리즘이다.

DFS로 위에서 주어진 노드 방문 순서는 아래와 같다.

처음 방문한 노드를 기준으로 모든 경로들을 따라나간 뒤, 다음 노드를 방문한다.

DFS는 스택을 사용하여 아래와 같이 구현할 수 있다.

1. 우선 빈 스택를 생성한 뒤 시작 노드를 추가한다.

2. 스택이 비어있지 않은 경우 아래 과정을 반복한다.

3. (Loop Start) 스택에서 pop한다.(스택의 Top에 있는 원소를 pop)

4. pop한 원소의 자식 노드들을 스택에 append한다. (Loop end)

5. 큐가 비어있으면 종료한다.

위의 코드를 구현해보면 아래와 같다.

def dfs(arr, start):
    visited = defaultdict(bool)
    stk = [start]
    answer = []
    while stk:
        x = stk.pop()
        if visited[x] == False:
            visited[x] = True
            answer.append(x)
            stk.extend(v_list[x][::-1])
    return answer

큐(Queue)는 데이터를 넣고빼는 자료구조 중 하나로, 먼저 삽입된 데이터가 먼저 추출되는 FIFO(First In First Out) 구조를 가지고 있다. 큐는 Front, Rear라는 두개의 포인터를 사용하여 데이터를 관리한다.

Front : 다음 추출될 데이터를 가리킨다.

Rear : 다음 데이터가 저장될 공간을 가리킨다.

데이터를 삽입하는 행위를 enque, 추출하는 행위를 deque라고 부른다. enque 및 deque 실행 시 포인터 관리에 유의해야 한다.

(구현 방법에 따라 포인터의 증감 순서는 조금씩 다를 수 있다.)

1. 변수

  1) Capacity : 크기

  2) Front : 큐의 맨 앞

  3) Rear : 큐의 맨 뒤

  4) No : 큐에 들어있는 데이터의 갯수

2. 함수

  1) enque() : 큐에 데이터를 넣는 함수

  2) deque() : 큐에서 데이터를 빼는 함수

  3) __len__() : 큐에 넣어있는 데이터의 갯수를 반환하는 함수

  4) dump() : 큐 안에 있는 데이터를 순차적으로 모두 읽는 함수

  5) peek() : 맨 앞 데이터를 들여다보는 함수

  6) find() : 큐에서 특정 값을 찾아 인덱스를 반환하는 함수

  7) count() : 큐 안에서 특정 값의 갯수를 찾아 반환하는 함수

  8) contains() : 큐 안에 특정 값의 존재 여부를 찾아 반환하는 함수

  9) clear() : 큐를 초기화하는 함수

  10) is_full() : 큐가 가득 찼는지 확인하는 함수

  11) is_empty() : 큐가 비었는지 확인하는 함수

3. Exception

  1) Empty : 큐가 빈 경우 발생하는 Exception

  2) Full : 큐가 가득 찬 경우 발생하는 Exception

* 구현 내용

class FixedQueue:
    
    class Full(Exception):
        pass

    class Empty(Exception):
        pass

    def __init__(self, c : int):
        self.capacity = c
        self.front = 0
        self.rear = 0
        self.no = 0
        self.queue = [None] * self.capacity

    def is_full(self) -> bool:
        if self.no >= self.capacity:
            return True
        else:
            return False

    def is_empty(self) -> bool:
        if self.no <= 0:
            return True
        else:
            return False

    def enque(self, data):
        if self.is_full():
            raise FixedQueue.Full
        self.queue[self.rear] = data
        self.rear += 1
        self.no += 1
        if self.rear == self.capacity:
            self.rear = 0

    def deque(self):
        if self.is_empty():
            raise FixedQueue.Empty
        r_data = self.queue[self.front]
        self.front += 1
        self.no -= 1
        if self.front == self.capacity:
            self.front = 0
        return r_data
        
    def __len__(self):
        return self.no

    def dump(self):
        if self.is_empty():
            print('큐가 비었습니다.')
        else:
            for i in range(self.no):
                print(self.queue[(i + self.front)%self.capacity])

    def peek(self):
        if self.is_empty():
            raise FixedQueue.Empty
        return self.queue[self.front]

    def find(self, value):
        for i in range(self.no):
            idx = (i + self.front) % self.capacity
            if self.queue[idx] == value:
                return idx
        return -1

    def count(self, value):
        c = 0
        for i in range(self.no):
            idx = (i + self.front) % self.capacity
            if self.queue[idx] == value:
                c += 1
        return c

    def contains(self, value):
        return self.count(value)

    def clear(self):
        self.no = 0
        self.front = 0
        self.rear = 0

www.acmicpc.net/problem/2493

탑들이 일렬로 서있다. 각 탑의 꼭대기에서 왼쪽을 보았을 때, 높이가 같거나 높은 가장 가까운 탑을 출력하는 문제이다. 만약 없다면, 0을 출력한다.

* 힌트

1. 스택을 활용한다.

2. i번째 탑의 높이보다 i+1번째 탑의 높이가 높다면, i번째 탑은 i+1번 이후 탑들의 신호를 수신하지 못한다.

* 풀이

스택을 생성하고, 신호를 수신할 가능성이 있는 탑들은 스택에 추가한다. 

  1. 앞에서부터 순차적으로 탐색한다. 0<=i<len(tower_list)

  2. 스택이 비었을 때는 수신 가능한 탑이 없다는 뜻이므로 0을 출력하고 스택에 i번째 탑의 [높이, index]를 추가한다. 

  3. 스택이 비지 않았다면, 스택에 들어있는 탑들에 대하여 높이가 현재 탑의 높이보다 같거나 높은지 비교한다.(현재 탑의 신호를 수신할 수 있는지 확인)

  4. 현재 탑보다 높이가 낮은 것은 스택에서 pop하고, 높은 것이 있다면 해당 탑의 Index를 출력하고 스택의 현재 탑을 추가한다. 스택 탐색을 멈춘다.

  5. 1~4번을 tower_list의 끝까지 반복한다.

* 예제  

탑들이 위 그림과 같이 주어져 있다.

각 탑들의 신호를 몇번째 탑에서 수신하는지 확인해본다.

첫번째 탑의 신호 : 받을 수 있는 탑이 없다. → 0을 출력

두번째 탑의 신호 : 받을 수 있는 탑이 없다. → 0을 출력

세번째 탑의 신호 : 두번째 탑이 수신한다.  → 2을 출력

네번째 탑의 신호 : 두번째 탑이 수신한다. → 2을 출력

다섯번째 탑의 신호 : 네번째 탑이 수신한다 → 4을 출력

정답 : 0 0 2 2 4

그럼 위의 예제를 실제 코드로 테스트해본다.

* Index에 주의 : 첫번째 탑의 Index  0* 

tower_list = [6, 9, 5, 7, 4]

[1] 첫번째 탑 : index = 0, 탑의 높이 = 6, 스택 = []

  1) 스택이 비어 있으므로, 스택에 [6(탑의 높이), 0(탑의 Index)]를 추가한다.

  2) 스택이 비어있다는 뜻은, index 0번 탑의 신호를 수신할 수 있는 탑이 없다는 것을 의미하므로 0을 출력한다.

output = '0'

[2] 두번째 탑 : index = 1, 탑의 높이 = 9 스택 = [ [6,0] ]

  1) 스택이 비지 않았으므로, 비교를 시작한다. 

  2) 스택의 첫번째 원소 : [6,0]

      현재 탑의 높이 : 9 > 6 이므로 첫번째 원소를 pop한다.

  3) 스택이 비었으므로 두번째 탑의 신호를 수신할 수 있는 탑은 없다.

     현재 탑의 높이와 인덱스를 스택에 추가한다.

output = '0 0'

[3] 세번째 탑 : index = 2, 탑의 높이 = 5 스택 = [ [9,1] ]

  1) 스택이 비지 않았으므로, 비교를 시작한다.

  2) 스택의 첫번째 원소 : [9,1]

      현재 탑의 높이 : 5 < 9 이므로 해당 탑에서 세번째 탑의 신호를 수신한다.

      높이 9인 탑의 index +1(2)를 출력하고, 현재 탑의 높이와 인덱스 [5,2]를 스택에 추가한다.

output = '0 0 2'

[4] 네번째 탑 : index = 3, 탑의 높이 = 7, 스택 = [ [9,1], [5,2] ]

  1) 스택이 비지 않았으므로, 비교를 시작한다. (스택의 오른쪽부터 탐색한다. 이는 가장 가까운 탑부터 탐색한다는 의미이다.)

  2) 스택의 첫번째 원소 : [5,2]

      현재 탑의 높이 : 7 > 5이므로, 해당 탑을 pop하고 다음 탑과 비교한다.

  3) 스택의 두번째 원소 : [9,1]

      현재 탑의 높이 : 7 < 9이므로, 해당 탑에서 네번째 탑의 신호를 수신한다.

      높이가 9인 탑의 index + 1(2)을 출력하고, 현재 탑의 높이와 인덱스 [7,3]을 스택에 추가한다.

output = '0 0 2 2'

[4] 다섯번째 탑 : index = 4, 탑의 높이 = 4, 스택 = [ [9,1], [7,3] ]

  1) 스택이 비지 않았으므로, 비교를 시작한다.

  2) 스택의 첫번째 원소 : [7,3]

      현재 탑의 높이 : 4 < 7이므로, 해당 탑에서 다섯번째 탑의 신호를 수신한다.

      높이가 7인 탑의 index + 1(4)를 출력하고 현재 탑의 높이와 인덱스 [4,4]를 스택에 추가한다.

최종 output = '0 0 2 2 4'

스택 : [ [9,1], [7,3], [4,4] ]

import sys
r = sys.stdin.readline

# 입력 받기
n = int(r())
t_list = list(map(int, r().split()))
answer = []
stk = []
for i in range(n):
    h = t_list[i]
    if stk:
        #print(stk)
        while stk:
            if stk[-1][0] < h :
                stk.pop()
                if not stk:
                    print(0, end=' ')
            elif stk[-1][0] > h:
                print(stk[-1][1]+1, end=' ')
                break
            else : 
                print(stk[-1][1]+1, end=' ')
                stk.pop()
                break
        stk.append([h, i])
    else:
        print(0, end=' ')
        stk.append([h,i])

 

www.acmicpc.net/problem/9012

괄호의 조합들을 입력받았을 때, 쌍이 제대로 맞으면 'YES', 아니면 'NO를 출력하는 문제이다.

* 힌트

1. 스택의 개념을 사용한다.

* 풀이

end = 0

1. 입력을 받아 차례로 스택에 넣는다.

2. 스택의 원소들을 하나씩 pop하며 아래 조건에 따른다.

  1) pop한 원소 = ')'

     : end + 1 을 해준다.

  2) pop한 원소 = '('

     : end - 1을 해준다.

  3) end <0일 경우 break

3. for문이 끝났을 때 end가 0인지 확인한 후 0이면 'YES', 아니면 'NO'를 출력한다.

해당 문제는 알고리즘 문제에 자주 등장하는데, 스택의 개념을 활용해서 풀 수 있다는 것을 처음 알았다.

import sys
r = sys.stdin.readline

n = int(r())
# (이면 end - 1
# )이면 end + 1
# 두번째 for문 내에서 end 가 0보다 작아지면 No를 출력하고, 마지막에 end가 0인지 확인한다.
for i in range(n):
    string = list(r().strip())
    end = 0

    for i in range(len(string)):
        x = string.pop()
        if x == ')':
            end += 1
        else:
            end -= 1
        if end <0:
            break
    if end !=0:
        print('NO')
    else:
        print('YES')
    

스택(Stack)은 데이터를 넣고 뺄 수 있는 자료구조의 형태 중 하나이다. 

스택에 데이터를 넣고 빼는 방법은 총알을 탄창에 넣고 총을 쏘는 것과 똑같다.

아래의 맨 왼쪽과 같이 빈 탄창과 총알 4개가 있다고 하자. 총알 4개를 1번부터 순서대로 넣으면 가운데 그림처럼 될 것이다. 이후 총을 쏘기 시작하면 맨 마지막에 넣은 4번 총알부터 발사가 될 것이다. 

  (탄창 = Stack, 총알 = Data) 과 같이 생각하면 된다. 스택에 데이터를 넣는 과정은 탄창에 총알을 넣는 과정과 동일하며, 스택에서 데이터를 빼는 과정은 탄창에서 총알이 발사되는 과정과 동일하다.

스택에 데이터를 넣는 행위를 Push, 스택에서 데이터를 빼는 행위는 Pull이라고 부른다. 4개의 데이터를 스택에 넣고 빼는 과정을 생각해보면, 가장 먼저 넣은 데이터(1번)이 가장 마지막에 나오는 것을 알 수 있다. 이런 데이터 구조를 FIFO(First In Last Out, = 선입후출)이라고 부른다. 

스택은 크기 제한(Top = capacity)을 가지고 있으며, 데이터는 맨 아래(Bottom)부터 꼭대기까지 하나씩 순차적으로 들어간다. 데이터를 꺼낼 때는 맨 위에서부터(가장 최근에 넣은 것부터) 하나씩 뺄 수 있다. 이제 해당 자료구조를 파이썬으로 구현하기 위한 함수, 변수들을 생각해보자.

* 변수

1. 스택 포인터(ptr)

 : 현재 스택에 데이터가 어디까지 쌓여있는지 나타내는 포인터. 

2. 크기(capacity)

 : 스택의 크기를 나타내는 변수. 스택 생성 시 지정해준다.

* 함수

1. __init__() : 변수 초기화

2. push() : 스택에 데이터를 한개 삽입한다.

3. pop() : 스택에서 데이터를 한개 꺼낸다.

4. __len__() : 현재 쌓여있는 데이터의 크기를 반환한다.

5. is_empty() : 스택의 empty 여부를 확인한다.

6. is_full() : 스택이 가득 찼는지 확인한다.

7. peek() : 가장 최근에 쌓인 데이터를 읽는다.

8. clear() : 스택을 초기화한다.

9. find() : 스택 내에서 특정 값을 찾는다.

10. count() : stack에 있는 특정 값의 개수를 찾는다.

11. contains() : 특정 값을 포함하고 있는지 확인한다.

12. dump() : 스택 내의 모든 데이터를 출력한다.

구현은 아래와 같다. 스택 포인터(ptr)이 작동하는 방식을 잘 봐야 한다.

1. 스택 포인터는 항상 빈 공간을 가리키고 있다.

2. 포인터의 위치만을 수정하여 스택초기화, 데이터 제거가 가능하다.

#Fixed스택 직접 구현해보기
from typing import Any

class FixedStack:
    ##Stack Pointer는 미리 다음 빈 공간을 가리키고 있다.

    class Empty(Exception):
        pass
    class Full(Exception):
        pass

    def __init__(self , c : int) -> None:
        ## 변수 초기화 함수.
        ## stack의 크기를 생성 시 전달받는다.
        self.ptr = 0
        self.capacity = c
        self.stk = [None] * c

    def __len__(self) -> int:
        ## Stack의 길이를 반환하는 함수
        ## ptr은 다음 빈 공간을 가리키고 있기 때문에 길이와 같다.
        return self.ptr

    def is_empty(self) -> bool:
        ## Stack이 비었는지 확인하는 함수
        return self.ptr <= 0

    def is_full(self) -> bool:
        ## Stack이 가득 찼는지 확인하는 함수
        return self.ptr >= self.capacity

    def push(self, data: int) -> None:
        if self.is_full():
            raise FixedStack.Full
        self.stk[self.ptr] = data
        self.ptr += 1
    
    def pop(self) -> any:
        ## Stack의 가장 바깥에 쌓여있는 데이터를 Stack에서 빼는 함수.
        ## 비었는지 확인하고 data를 return한다. 이 때 ptr만 하나 줄여주면 된다.
        if self.is_empty():
            raise FixedStack.Empty
        self.ptr -= 1
        return self.stk[self.ptr]

    def peek(self):
        ## 가장 바깥에 쌓여있는 데이터를 읽어오는 함수
        ## 비어있는지 확인 후 data를 return한다.
        if self.is_empty():
            raise FixedStack.Empty
        return self.stk[self.ptr-1]

    def clear(self):
        ## Stack을 초기화하는 함수
        self.ptr = 0
    
    def find(self, value: Any) -> Any:
        ## 전달받은 값을 찾는 함수.
        ## 찾으면 index를 반환한다.
        for i in range(self.ptr - 1, -1, -1):
            if self.stk[i] == value:
                return i
        return -1

    def count(self, value : Any) -> int:
        ## Stack 안에 찾고자 하는 값이 몇개인지 찾는다.
        count = 0
        for i in range(self.ptr):
            if self.stk[i] == value:
                count += 1
        return count

    def __contains__(self, value: Any) -> bool:
        ## Stack이 특정 값을 포함하고 있는지 확인하는 함수
        return self.count(value)

    def dump(self) -> None:
        ## 데이터를 바닥부터 꼭대기까지 출력한다.
        ## ptr까지 출력해야 하는 이유는 그 뒤에 삭제하지 않고 남은 데이터가 있을 수도 있기 때문!
        if self.is_empty():
            raise FixedStack.Empty
        else:
            print(self.stk[:self.ptr])
        

https://www.hackerrank.com/challenges/frequency-queries/problem?h_l=interview&playlist_slugs%5B%5D=interview-preparation-kit&playlist_slugs%5B%5D=dictionaries-hashmaps

[ 문제 ] 주어지는 query들을 정해진 규칙에 따라 수행하고 최종 출력을 return한다.

query 형태 = [a,b]

a에 따라 수행 작업이 달라지며, b는 수행의 대상이다.

arr, output = []

1) a = 1 : b를 arr에 넣는다.

2) a = 2 : b를 arr에서 뺀다.(존재할 경우)

3) a = 3 : list에서 frequency가 b인 것이 존재할 경우 1을, 존재하지 않을 경우 0을 output에 넣는다.

[ 예시 ]

[ 방법 ] : 리스트를 만들지 않고 dictionary로 처리한다.

dict = {}

output = []

1. query를 읽는다.

query[0] = a

query[1] = b

   1) a == 1일 경우 : dict[b]에 1을 추가한다. 

   2) a == 2일 경우 : dict[b]에서 1을 뺀다.

   * 이 때, dict[b]가 음수가 되어서는 안된다.

   3) a == 3일 경우 : dict.values()에 b가 있다면 1을, 없다면 0을 output에 추가한다.

간단한 문제이지만 Time out으로 해결되지 않는 case도 있어서 몇가지 Trick을 추가해줘야 합니다-!

https://www.hackerrank.com/challenges/count-triplets-1/problem?h_l=interview&playlist_slugs%5B%5D=interview-preparation-kit&playlist_slugs%5B%5D=dictionaries-hashmaps

간단해 보이지만 어김없이 시간 제약에 걸리는 문제입니다.

문제 : 숫자 리스트 arr과 공비 r이 주어졌을 때,

arr[i] = 임의의 숫자 k

arr[j] = k * r

arr[k] = k * r * r

를 만족하는 (i,j,k)의 총 갯수를 구하는 문제입니다. 이 때 i < j < k를 만족해야 합니다.

예를 들어,

arr = [1, 2, 2, 4] , r = 2라고 할 때

arr[0] = 1, arr[1] = 2, arr[3] = 4 (i = 0, j = 1, k = 3)

arr[0] = 1, arr[2] = 2, arr[3] = 4 (i = 0, j = 2, k = 3)

라는 두개의 해를 찾을 수 있습니다. 

방법 : 저는 찾아야 하는 3개의 숫자 중 가운데 숫자(arr[j])를 기준으로 i,j,k의 조합을 찾아내기로 했습니다.

* arr[j]의 특성은 r로 나눴을 때 나머지가 0이라는 점입니다.(arr[k]도 마찬가지긴 합니다.)

1) Counter 라이브러리를 활용하여 arr의 구성 요소에 대한 dict를 생성한다.

2) 빈 라이브러리 dict2를 생성한다.

3) 리스트에 대해 for loop을 돌리면서 나오는 숫자(num)가 r로 나눴을 때 나머지가 0인지 확인한다.

  3.1) 나머지가 0이 아닌 경우 : dict2[num]에 1을 더하고, dict[num]에 1을 빼준다.

  3.2) 나머지가 0인 경우 :

          1) dict2[num//r]이 존재하고, dict[num*r]이 존재할 경우, 정답에 dict2[num//r] * dict[num*r]을 더한다.

          2) 위의 둘 중 하나가 없는 경우 dict2[num]에 1을 더하고, dict[num]에 1을 빼준다.

위의 작업을 리스트의 처음부터 끝까지 반복하면 정답을 구할 수 있습니다 -!